B站原视频

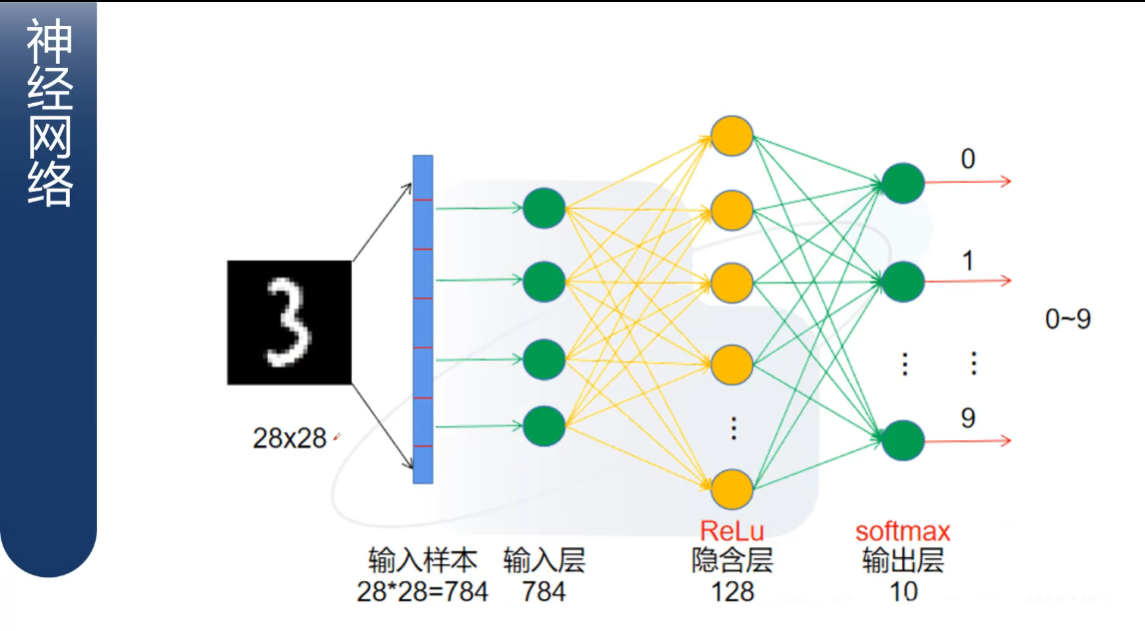
神经网络计算原理

ReLu函数作用：值小于零则输出0，大于零则输出其本身。

softmax函数作用 ：得出最终的概率值。
1、输入样本向量化，变成784个值的向量，这里的每个值就是输入层。

2、隐含层可以有多个参数、也可以有多层。

3、从上一层到下一层的过程为上一层的参数值乘一个系数，得到的值为下一层（这个值先称作计算值）。

4、以识别数字为例（便于理解），我们会给输出层设置一个结果（即可能的结果，先称作设定值-这是一个类别，也可以是别的，不一定是某个数字），到达输出层以后，计算值会变成e的几次方，最后输出层下一步获得的结果为每一个输出层对应结果的比例，也就是概率。-初步猜测可能是对概率进行识别对应的。当我们使用计算值得出的概率最大时，我们取这个计算值对应的设定值为输出结果（即下图3处，通过“1”来表示正确）。最后看其对应的概率。如果其概率为最大，则说明我们此次神经网络计算的结果正确，并记下此概率作为正确的概率。（只能说明这次的神经网络计算使用的参数正确的概率最高，还需要后续优化找到最高的。）

5、最后进行反向传播，并使用损失函数（CEloss-交叉熵损失）进行验证，若此时对应的损失函数值非最小（如下图），则需要降低梯度，反向传播，更新我们层与层之间计算时对应的参数，直至得到一个损失的最小值。此中原理后续会通过代码来表示。

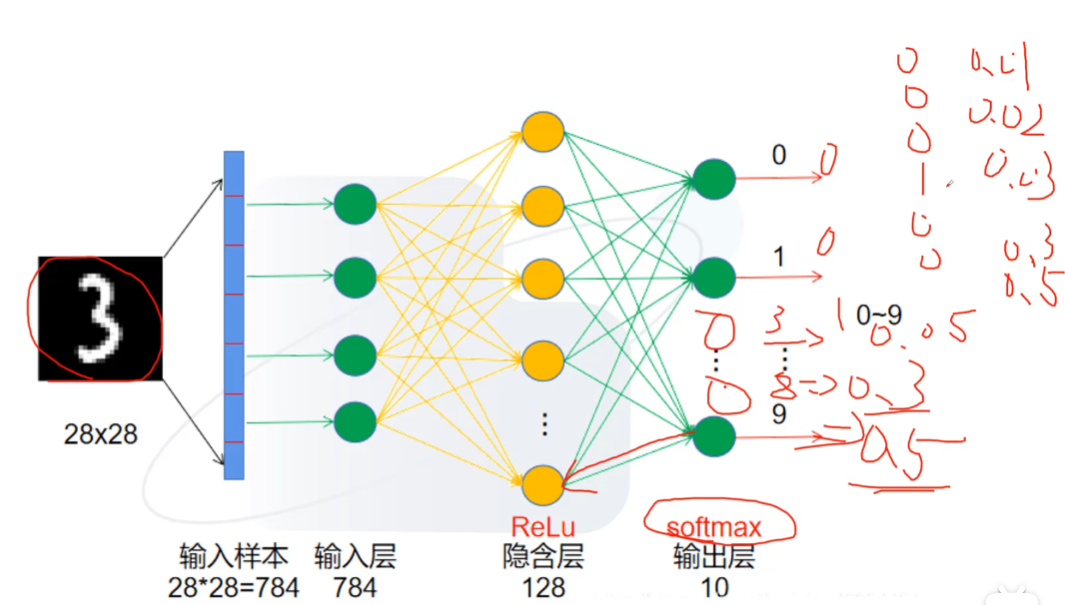
优化好后结果如下图

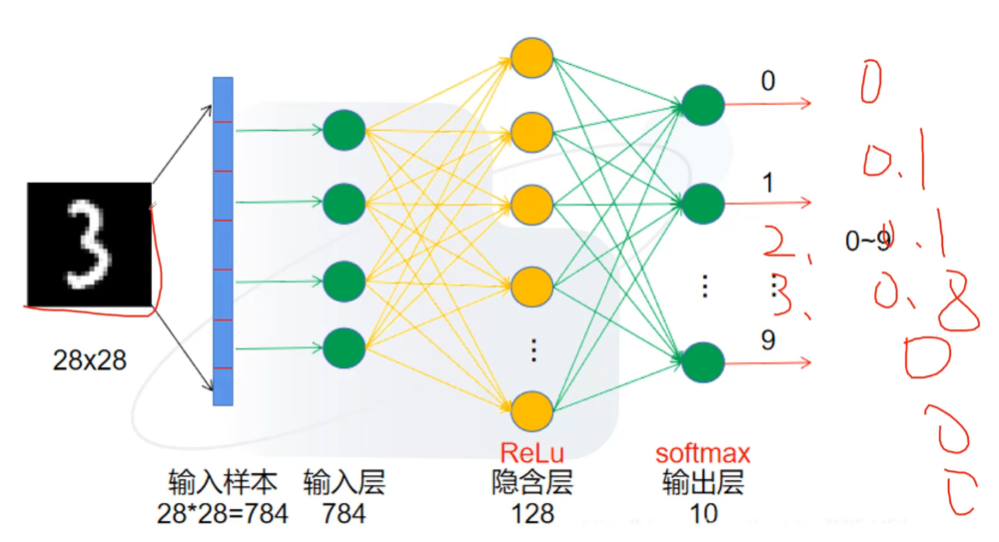
神经网络训练原理

batch操作：就是基础数据，用来训练的。最后获得一个最佳的参数（best_Pth），并存储起来，之后使用此参数进行计算/验证。

卷积神经网络

卷积理论

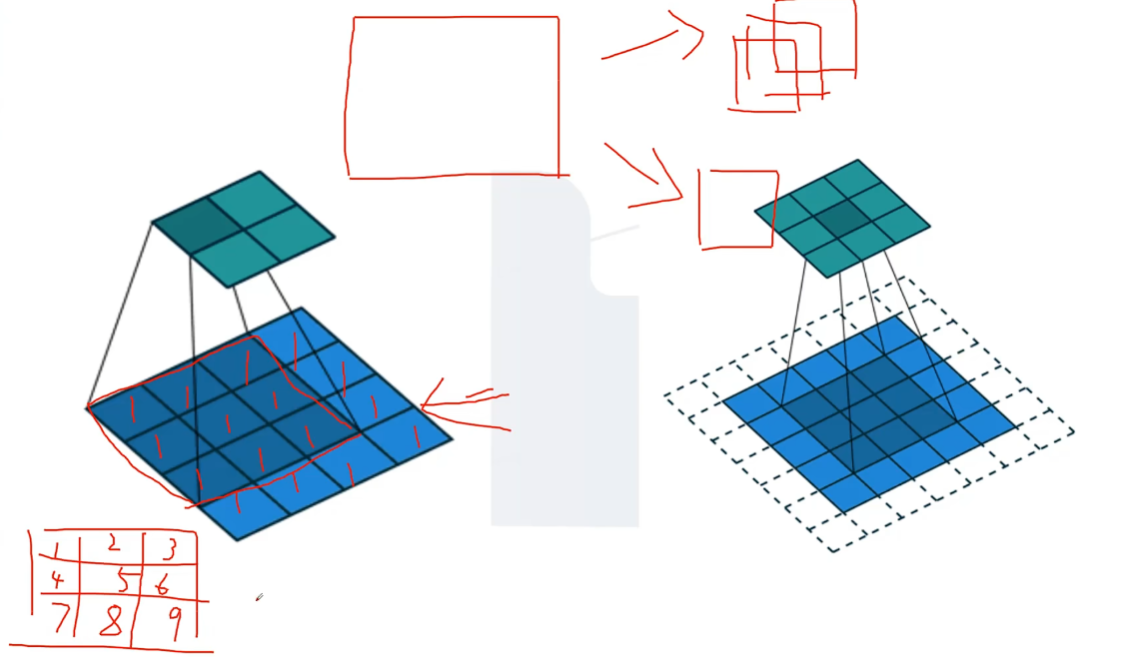
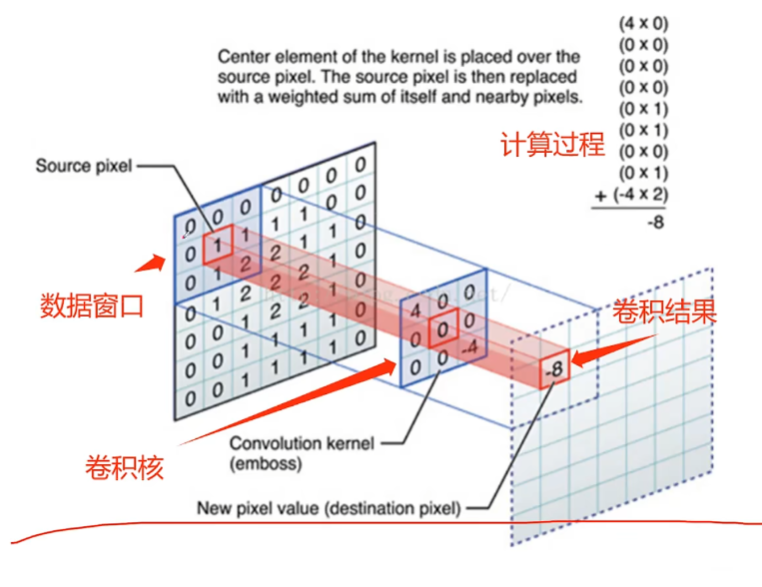
总体思想：每一个像素对应一个色度值，每个色度值（数据窗口）在映射一个块时（如左上角），九个格子里每个格子都会对应一个参数（卷积核），我们训练的对象，就是这个参数。

最后左上角的一个格子里的值为9个格子对应位置颜色值和参数的乘积之和。即45.

填充，填充（Padding）P=1为填充；一圈，并设定其颜色值（数据窗口）为0

梯度下降法

损失函数-即误差

这个（a，b）是模型的参数。要使用这两个参数进行计算。后续的每个点（a_n，b_n）的模型损失，都会小于起始点（a₀,b₀）。因此只要按照最后一行的迭代算法对a，b进行迭代，最后利用a，b计算得到的ΔL都会小于前一个ΔL，也就是误差在越来越小（md数学知识很久没学了）。

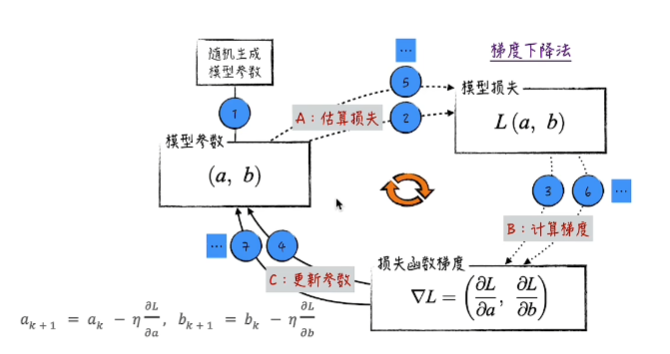
此图为梯度下降法的原理，这个流程叫向前传播（按照流程进行计算）